前回、相加相乗平均の不等式の話をしたときに思い出した問題がありましたので、今回はそれを取り上げてみたいと思います。
2002年の宮崎大学の問題です。

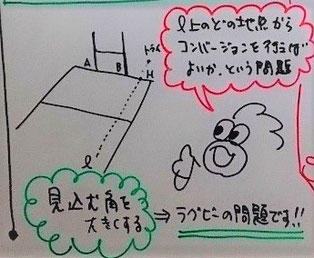
これを見てラグビーの問題と気づく人もいるのではないでしょうか。つまり、図のH地点でトライが決まったとき、その後のキック(コンバージョンキック)は、直線l上の任意の地点から行うことができます。AとBのポールの間を通せば成功ということなので、できるだけABを見込む角が大きいところから蹴ればいいわけです。その地点Pを決定する問題だったんですね。
ではまず普通に解いてみましょう。


得られた答えがaとbの相乗平均になっているところが美しいですね。では、この問題を図形的に考えてみましょう。


① A,Bを通る円を考える
② 図Ⅰにおいて、∠AQB<∠APB となる
③ よって、図ⅡのようにA,Bを通り、lに接する円を描けば、その接点Pがθの最大値を与える点である
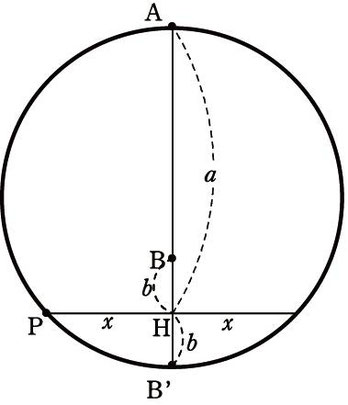
Pの位置の決定の仕方を一つ示しておきたいと思います。
まず、直線lに対するBの対称点B’を取ります。次に、AB'を直径とする円を考えます。この円とlが交わった点がPとなります。これは方べきの定理を利用して平方根の作図を行う方法です。b=1とすれば任意の√aの作図ができるわけですね。
因みにこの円の直径はa+bなので、半径はその半分、つまりa,bの相加平均になりますね。図から(相加平均)≧(相乗平均)が言えますし、等号成立はa=bのときであることもわかりますね。
コンバージョンキックをする選手はこんなイメージを持っていれば、見込む角を最大にするポジションがわかるわけです。ってそんなことする選手なんかいませんよね。

コメントをお書きください