ワンポイント数学講座
ワンポイント数学講座 · 2024/04/21
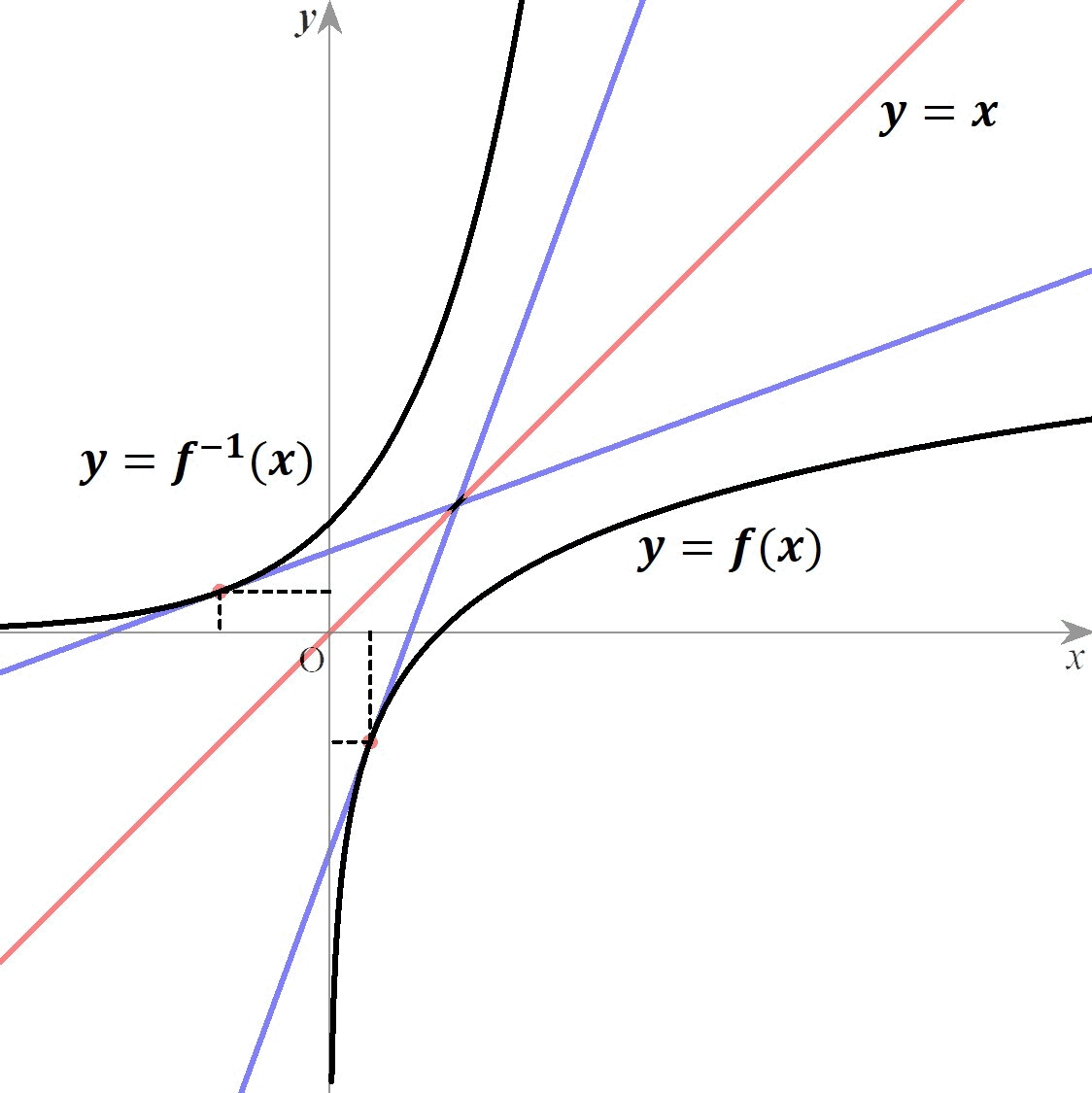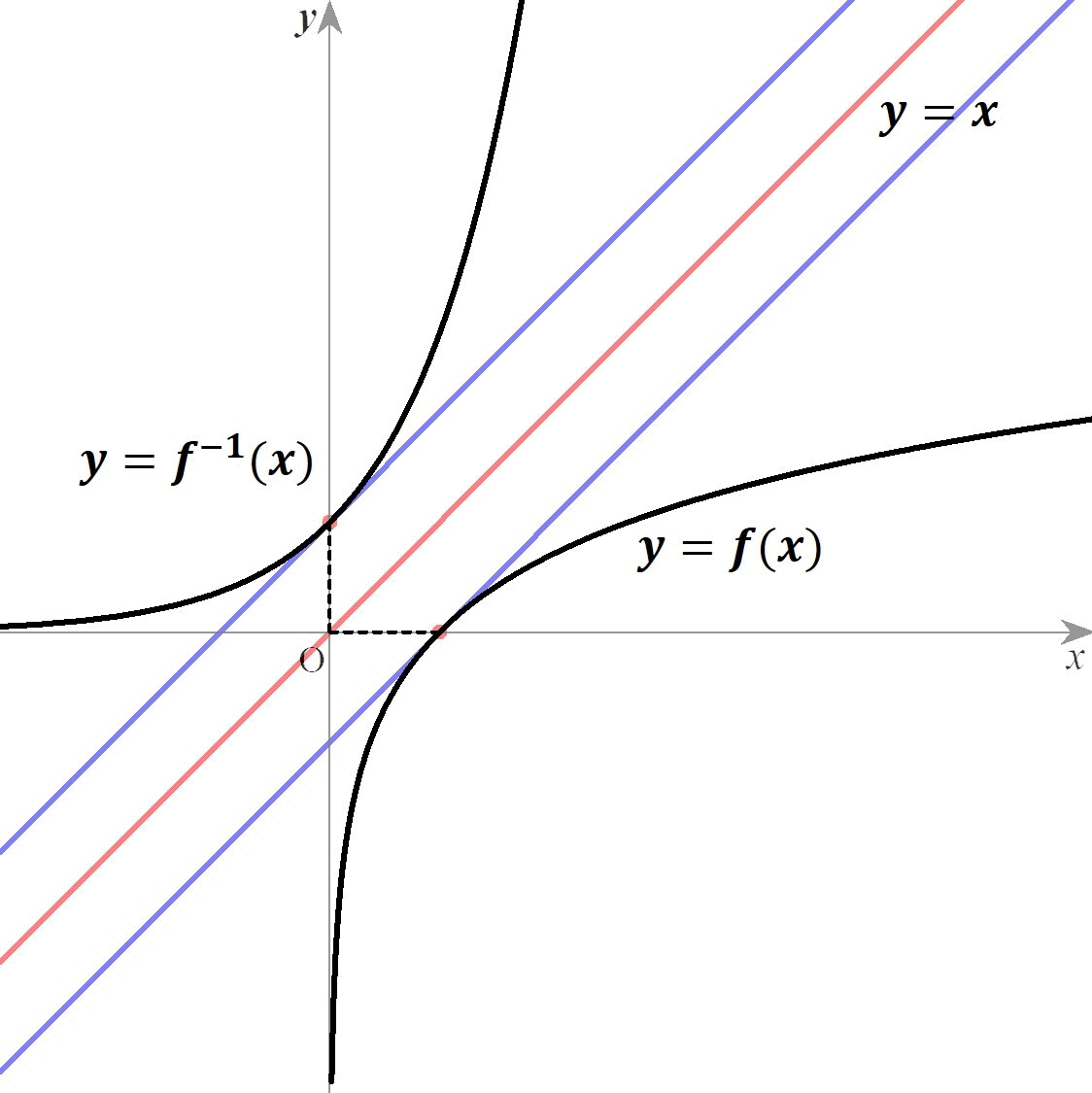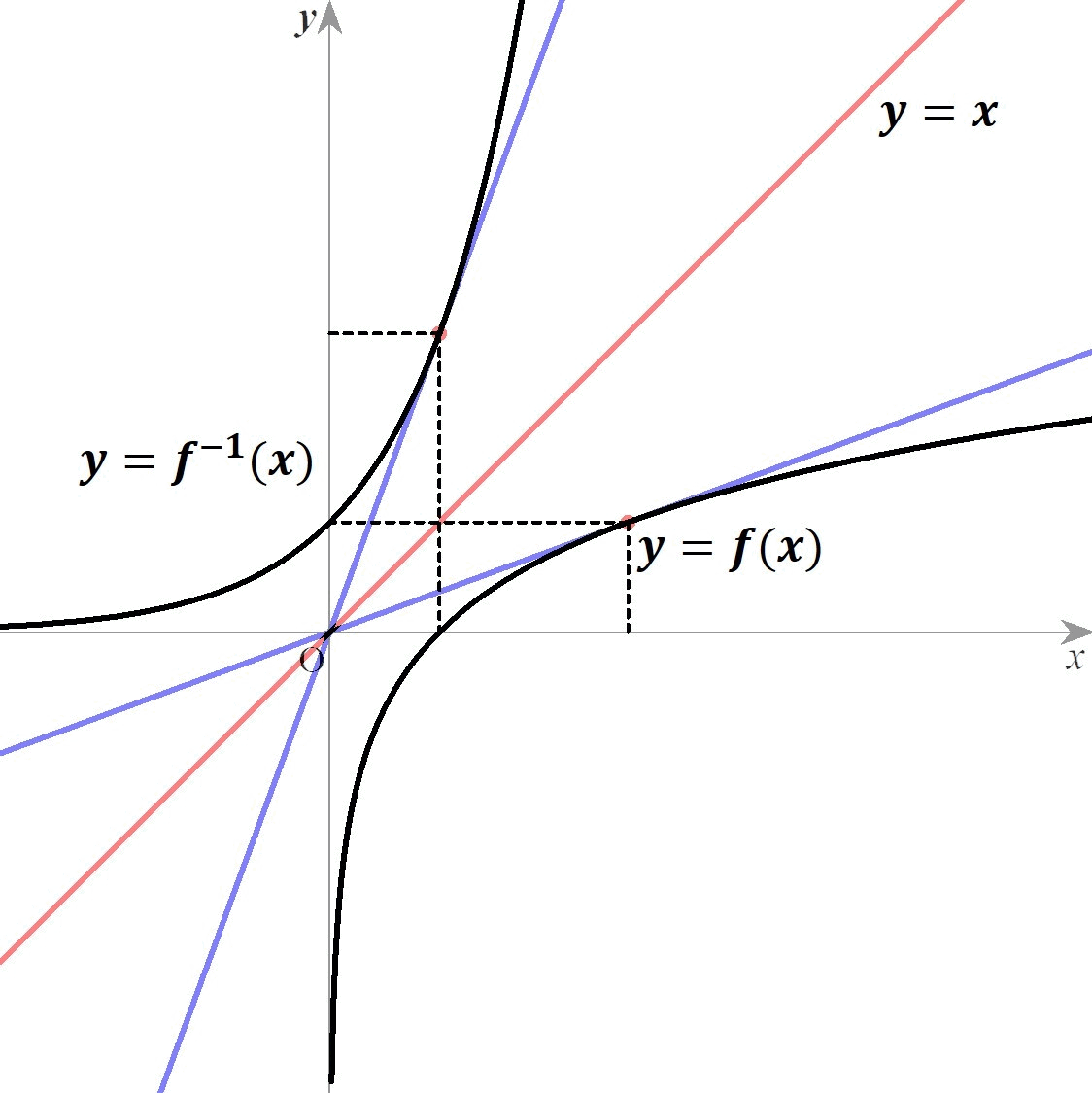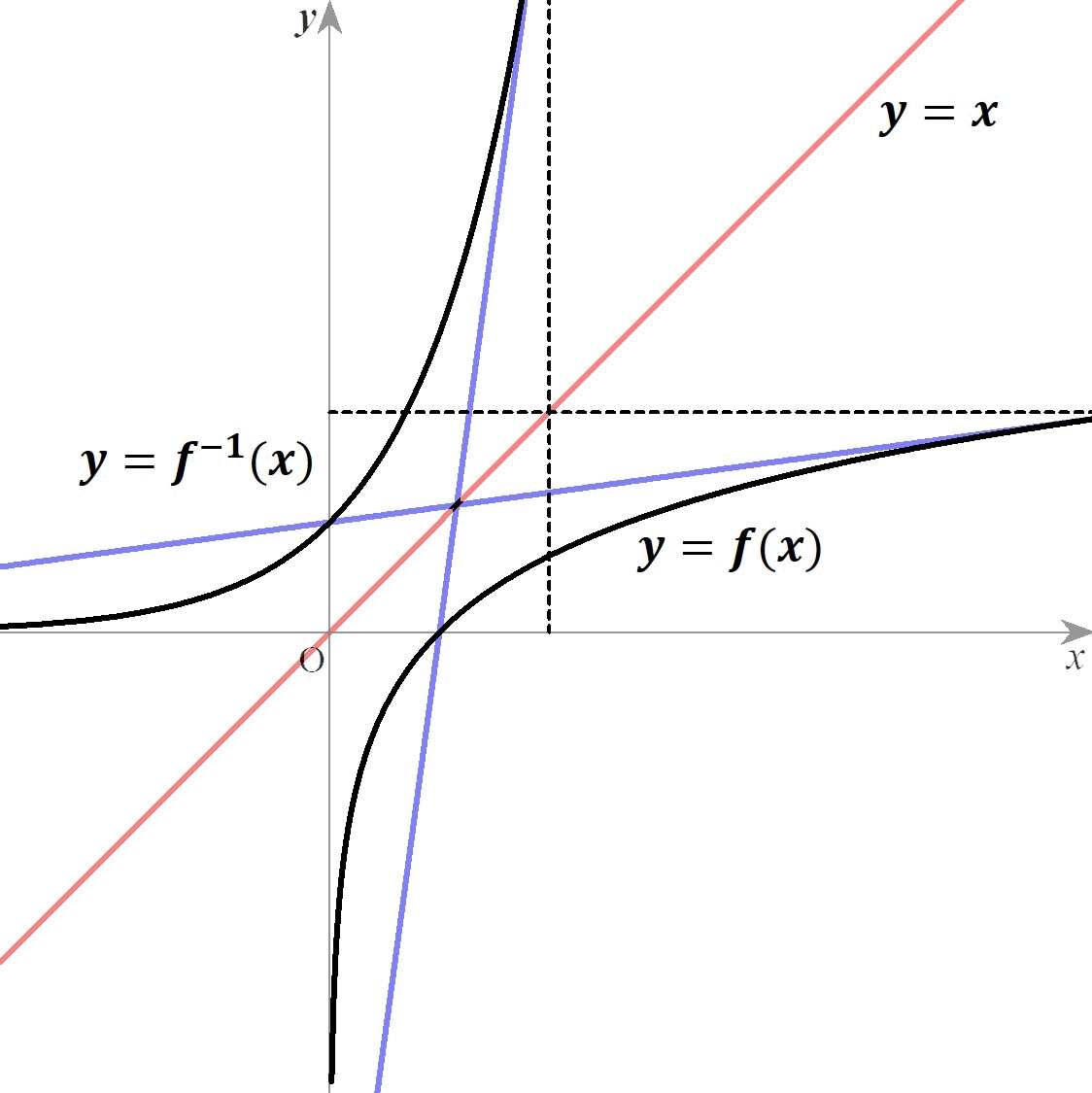
関数と逆関数の、対応する点における接線の傾きが逆数になっている。 つまり がいえる。 The function and the inverse function have reciprocal tangent slopes at the corresponding points.
ワンポイント数学講座 · 2024/03/19
カーテンがだんだん閉まっていくイメージです。 右端が最小値になる場合と、頂点が最小値になる場合に分けて解答を作りましょう。 It is an image of the curtain gradually closing. Let's make a separate answer for the case where the right edge is the minimum value and when the vertex is the minimum value.
ワンポイント数学講座 · 2024/03/19
aの値が変化するとき、赤い帯の部分に注目すると、最小値は左端、頂点、右端と変化している。これらを場合分けして解答としてまとめればよい。 When the value of a changes, if you pay attention to the red band, the minimum value changes to the left edge, the vertex, and the right edge. These can be divided into cases and summarized as answers.
ワンポイント数学講座 · 2022/12/03
昨日は昨日はサッカー日本代表やりましたね。スペインを2-1で破り見事決勝トーナメント進出を果たしました。ところで、サッカーボールといえば「フラーレン60」です。 フラーレン60とは、12個の正五角形と20個の正六角形の分子構造を持つ炭素の同素体で、右図のようなサッカーボールの形をしています。
ワンポイント数学講座 · 2022/01/19
大学入試共通テストの数学Ⅰ・Aの評判がすこぶるよくないようです。計算量が多く、時間内に完答するのは至難の技とのこと。それで、私もようやくというか、遅きに失しているわけではありますが、先ほど問題を解いてみました。なるほど~。聞きしに勝る面倒さ。告白するとわたしゃあ60分で解けませんでした。しかも、電卓を叩くという反則も犯しちゃいました。それでも満点いけませんでした。 解いてみて頭に浮かんだのは、アップル社CEOのティムクックが、MITの卒業式で語った言葉です。「私はコンピューターが人間のような思考することなんて恐れない。それより、人間がコンピューターのようにふるまうことのほうが恐ろしい」というやつ。 AIが人間に取って代わられるといわれて久しいですが、どうやら今回の問題が意図したのは、人間がAIに取って代わろうという挑戦なのかもしれません(笑)。なぜって、ここで求められる能力は、例示された解き方を理解し、それと同様のテイストで後続に展開される拡張された設問に忠実にリフレインさせる力、面倒な四則計算をうんざりせずに黙々と正確にやりこなす力、などのように思えるからです。これを「一般化・抽象化する応用力」「やりきる力・グリッド」いわれれば、私はひたすら「とほほ」なわけですが。 ただ、この問題から(歯を食いしばって)私がポジティブなメッセージとして受け取ったのは次のことです。 グラフ描画ソフトなどを授業で活用せよ 過去問演習にひたすら時間をかけるとか、「これは出る」などといった「対策型」授業はやめませんか 日本が世界に誇る「算盤」を復活させ暗算力を強化しよう(いや、これってポジティブかな?) 恐らく(好意的に見ると)大学入学共通テストから今の授業を変革させるという思いがあるのかもしれませんね。 では、以下に、私の解答からちょっとだけエピソードを紹介したいと思います。