　昨日は昨日はサッカー日本代表やりましたね。スペインを２－１で破り見事決勝トーナメント進出を果たしました。ところで、サッカーボールといえば「フラーレン60」です。

　フラーレン60とは、12個の正五角形と20個の正六角形の分子構造を持つ炭素の同素体で、右図のようなサッカーボールの形をしています。

　先日中学1年生の授業に、ポリドロンという教具を持って行って「正多面体がなぜ5種類しかないか」というテーマで話をしました。その授業後に、「サッカーボール作ってみて」と言い残したところ、翌日教室にしっかりとフラーレン60ができていました。正六角形のフレームが足りないところを正三角形6個つなげて補っていますね。さすが！

　そこで、一昨日はこの模型を使って正多面体とフラーレン60の「面の数、頂点の数、辺の数」を数え上げる授業を行いました。ではその様子を以下に記しておきます。

ポリドロンを使う

まず正多面体の頂点と辺の数をポリドロンを用いて求めてみましょう。

正多面体（凸正多面体）は次の２つで定義されます。

①すべての面が同じ正多角形でできている。

②どの頂点にも同じ数だけの正多角形が集まっている。

この考えから、ポリドロンを使うと正多面体の辺の数と頂点の数を容易に求めることができます。

１　正四面体の場合

　下の写真で示すように、正四面体は４つの正三角形を集めて作られます。これら４つの正三角形の辺の数を合計すると

　3本×４個＝12本となります。ここで、この４つの正三角形で正四面体を作ると、各辺は必ず２つの三角形の辺が重なっていることがわかります。ということは、正四面体の辺の数は、三角形全部の辺の総数の半分ということになりますね。つまり、12÷2＝6本となります。

　次に正四面体の頂点の個数を考えましょう。まず、４つの三角形の頂点の総数は3個×４個＝12個ですね。ところが、正四面体を作ると、どの頂点にも３つの三角形が集まっていることがわかります。ということは、正四面体の頂点の個数は　　

　12÷3＝４個となりますね。

２　正六面体の場合

同様に正六面体の場合についても示します。各頂点に正方形が3個集まっています。

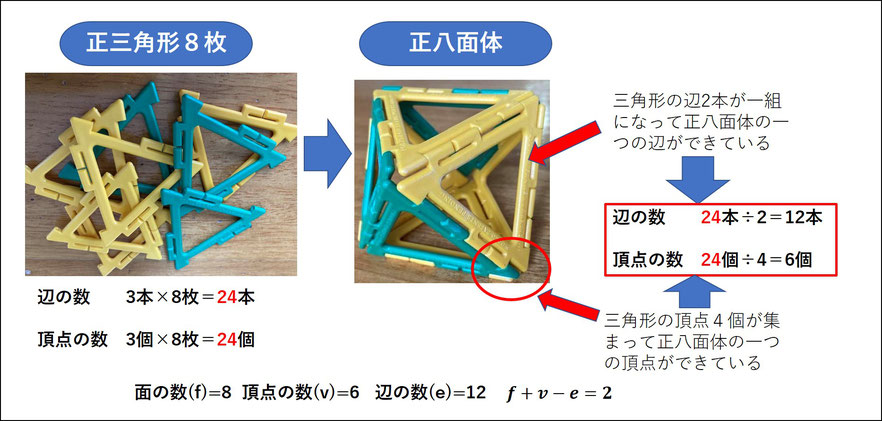
３　正八面体

正八面体は頂点に4枚の正三角形が集まっていますね。

４　正12面体

こちらは正五角形が３つ集まっています。

５　正二十面体

正三角形が５つ集まっていますね。

６　フラーレン60

　では、フラーレン60の頂点と辺の数を求めてみましょう。ポリドロンで作ったフラーレンをバラバラにすると、12個の正五角形と20個の正六角形でできていることがわかります。すると、辺の総数は

　5本×12個＋6本×20個＝180本となりますね。それを2で割ったものが、立体の辺の数なので、フラーレン60の辺の数は

90本であることがわかります。

　次に頂点を求めます。それぞれの正多角形の頂点の総和も180個ですね。立体の頂点を見ると、3個の正多角形が集まっているので、180÷3＝60個となります。

　あるいは、このフラーレンから正五角形をはずして、正六角形のフレームで考えて、6本×20個÷2＝60個としてもようでしょう。

　ポリドロンはなかなかいい教材ですね。

見取り図から求める

では次に、正多面体の見取り図から頂点と辺の数を求める方法を示します。

１　正六面体の場合

　下の板書写真を見てください。正六面体の見取り図のポイントは正六角形のシルエットです。頂点の個数は次のように考えます。まず縁にある頂点を数えましょう。6個ありますね。これらの点は裏面から見ても同じように見えます。次に図形の内部にある点を数えます。1個ですね。これは裏面からは見えませんが、裏面でも同じ構造の図が見えているはずなので、やはり内部にも点が1個あるはずです。

　このように考えると、頂点の総数は、(縁に見える点の個数)＋２×(内部に見える点の個数)　と求められますね。

　辺の数も同様です。縁の辺と、内部の辺の数を数えて、(縁に見える辺の本数)＋２×(内部に見える辺の個本数)とすればいいですね。