パソコンで外接円を描く

もう四半世紀前の1996年の話ですが、ある数学関係の雑誌に「コンピュータ・数学・授業の三題噺」というタイトルで数学エッセイを書いたことがあります。当時私は、授業におけるパソコン活用と数学との相互関係には２つの側面があると考えていました。

一つは、パソコンを授業に取り入れることによって数学がよくわかるようになるということです。1996年といえば、windows95の登場でOSの転換があり、また、今は死語ですが、CAI（Computer-Assisted-Instruction）という言葉が流行したように、「教育の情報化」が教育課程審議会などで中心的に議論されていた時代です。ただ私は、コンピュータをティーチングマシン的に使い、決められた教科内容をひたすら教え込んでいくといった、チュートリアル型とかコースウェアなどといわれるような情報教育には全く意義を見出せませんでした。それよりもパソコンの処理の過程や結果から新たな知見や数学的発見を得るということに興味を抱いていて、そんなソフトウェアの開発にずいぶんと熱中しておりました。このようにコンピュータが数学に働きかけ、数学の理解を助けてくれるという関わり方を、私はCAM（Computer-Assisted-Mathematics）と秘かに定義していました。

さて、パソコン活用と数学との相互関係におけるもう一つの側面は、コンピュータの仕組みやプログラミングに、数学が役に立っていることを理解するということです。つまり数学がコンピュータを支援していることを知るという逆の関連です。私はこのことを、MAC（Mathematics-Assisted-Computer） と名付けました。例えば、PC上で立体のアニメーションを行うとき、その裏で、ベクトルの内積・外積、一次変換などの考えが駆使されていることを知れば、数学の有用性や学ぶ意義を感じるのではないかということです。

では、そんなMACの一例として、三角形の外接円をパソコンで描画する授業の実践を以下にまとめてみたいと思います。

平面上の任意の3点の座標を与えてできる三角形の外接円を描くプログラムを考えます。３つの座標を入力するたびに自動的に外接円が描かれるためには、外心の座標が、入力される３つの座標の数値の演算で決定されること、つまり、外心の位置ベクトルを求めることが必要となります。

私は次のように説明しました。

まず、上図において外心をE、△ABE，△BCE，△CAEの面積をそれぞれ、S1，S2，S3とします。

このとき、AEの延長とBCの交わる点をDとすれば、BD：DC＝S1：S2　なので、

また、AD：ED＝△ABC：△EBC＝(S1+S2+S3)：S3  より、AE：ED＝(S1+S2)：S3 となり、その結果、

面積を使って外心の位置ベクトルを表すことができました。

ここで、外接円の半径をRとして、三角形の面積の公式

などを使えば、

という結果が得られます。ということは、A,B,Cの座標が得られたときに、sin2Aなどの三角比の値がわかれば外心の座標が決定されることになります。sin2Aなどの値は以下の様な流れで導きます。

まず、2点間の距離の公式で3辺の長さを求め、それを使って余弦定理でコサインの値を求めます。すると、

からサインの値がわかります。サインとコサインがわかるので、倍角の公式から sin2A などの値が求まり結論に達します。

このようにして、外心の座標が求められたので、外接円の半径を正弦定理によって求めれば描画をすることができますね。

因みに、ここでは鋭角三角形について説明しましたが、鈍角三角形でも同様のことが言えますので、図を描いて確かめてみてください。

さて、この過程は、何の変哲もない直線型のプログラムによって記述できますが、注目して欲しいのは、外接円を描くまでに登場した三角比の公式の数々です。2点間の距離、面積の公式、余弦定理、正弦定理、相互関係の公式、2倍角の公式と、数Ⅰで習う三角比のほとんどが網羅されています。

三角比の授業を一通り行った後、その活用として、外接円を描くプログラムを作ってみる活動を入れてみるのも面白いのではないでしょうか。数学を学ぶ意義を感じてくれるかもしれません。

因みに、私が授業で実践したときは、basic（ubasic)というプログラミング言語を用いました。それは今は使えないので、プログラミングではないのですが、Grapesといグラフ描画ソフトを用いたものを参考までに以下に示しておきます。

なお、ここではオマケとして内心も同時に描画するようにしています。

ここまで述べたのは、パソコンに描画させるためにプログラムや、セッションを作るプロセスを通して、そこに「数学が働いている」ことを知るということです（MAC）。

では、今度は、そこで作ったプログラムを使って、具体的に数学の勉強をしてみましょう。

下図（左）の様な、Bを極とする2本の直線BA，BCと、Eを極とする2本の直線EF，EAの4本の直線を考えます。この図形をニュートンの完全四角形と呼ぶこともあります。ここで、4本の直線から3本の直線を選ぶ選び方の総数は4C3=4 通りなので4つの三角形ができます。具体的には、△BAC，△BFD，△EDC，△EFAですね。ではここで、４つの三角形の外接円を描いてみましょう。

すると、何と４つの外接円はただ1点で交わります（下図右）。

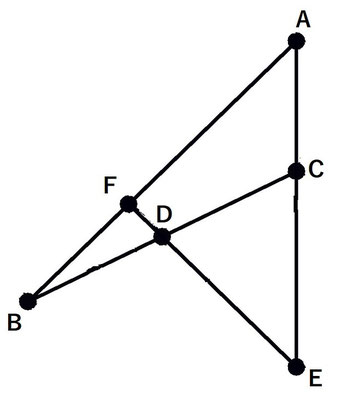
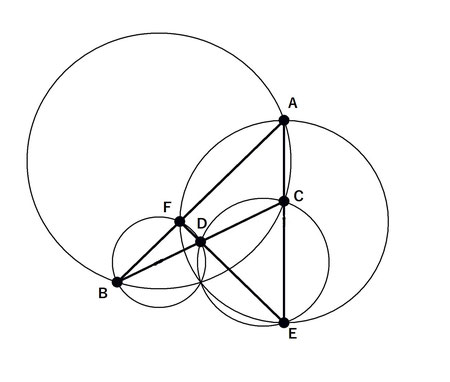
この図は、Grapesのスクリプト機能を使ってプログラミングしたものです。４つの三角形の座標を入力して次々に描画されます。

ではもうちょっと遊んでみましょう。下図（左）はペンタグラムを変形した星形図形です。これをよく見ると、５つの完全四角形で構成されていることがわかります。そこで、今星のとんがりの部分にある５つの三角形、△AFJ，△BGF，△CHG，△DIH，△HJIの外接円を描いてみましょう。すると、隣り合う２つの外接円の交点はそれぞれの完全四角形のスタイネル点ですね。

参考までに上の図の座標は次のようにしています。

A(5 , 5) , B(-3 , 5) , C(3 , -3) , D(5 , -5) , E(9 , 3) , F(3 , 3) , G(0 , 0) , H(1 , -1) , I(5 , 1) , J(5 , 3)

さて、ここで、５つのスタイネル点を見たときに何となく同一円周上にあるように思いませんか。私は試しに３つの交点の座標を目分量で求めて、試しに入力してみたところ、上右図のように確かに同一円周上にあるように見えました。

ここで、点を自在にグリグリ動かしてもその性質が変わらないことが見えるようにするには、ちょっと複雑なプログラミングになるので、これはGeoGebraとか、Cabri などの幾何ソフトで試してみたほうがいいですね。

事実、この５つのスタイネル点は必ず同一円周上にあることが知られていて、これをミケルの定理といいます。

このように、単純なプログラミングから数学の力を知り、そしてまた作ったソフトから発見的な学びが行うという循環が生まれれば数学をより楽しむことができるのではないかと思います。