もう30年以上前の話になりますが、デコパネで「ふすま」の教具を作ったことがありました。まずは下写真のようなパフォーマンスを行います。

写真①(クジラかな?)→写真②(鳥だ!)→写真③(ん?)→写真④(ウサギさん~)というカンジです。つまりフスマを少しずつ開けていくと様子が変わってくるというお話です。
さて、本題に入ります。この教具を作ったのは、関数において変域が変化する(右端がだんだん大きくなるタイプ)ときの最大値や最小値の見方をイメージするためなんですね。下写真を見てください。3次関数のグラフがだんだん現れていくときの最大値を追いかけていく様子です。

写真①→写真② 最大値はグラフの「右端」
写真②→写真③ 最大値はグラフの「極大値」
写真③→写真④ 最大値はグラフの「右端」
このような変化に気づきますね。
そこでポイントは、「右端」から「極大値」、「極大値」から「右端」への変わり目がどこにあるかということです。
実は3次関数では、x軸上において、極小値と同じ高さになる地点、極大値の地点、点対称の中心、極小値の地点、極大値と同じ高さになる地点、の5つの地点が等間隔で並ぶという、とてもステキな性質があります。下図を参照してください。
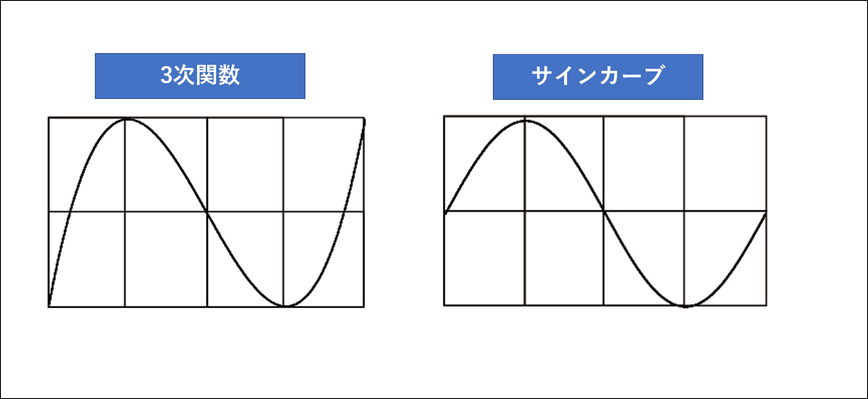
左が3次関数、一方参考までに右がサインカーブです。違いがわかりますね。このような3次関数の等間隔性、点対称性を称して「5点定理」とか、8個の長方形をつなげた形で示されることから「たたみ8畳の法則」などと呼んだりします。
でもこの性質を証明なしに結果だけ覚えて使うのはよろしくないですね。そこで、以前、ある生徒に説明するためにホワイトボードにまとめたときの写真を以下に紹介します。この方法が一番手っ取り早く示す方法かなと思います。

では、今回はここまで。
ご覧いただきありがとうございました。

コメントをお書きください